mm1Queue: a simple interactive M/M/1 queue simulator
Introduction
mm1Queue is a simple interactive M/M/1 queue simulator. It uses discrete time simulation and no threads. It is portable and easy to use. Ready-to-run Tcl/Tk source code is available, licensed under the GNU GPL.
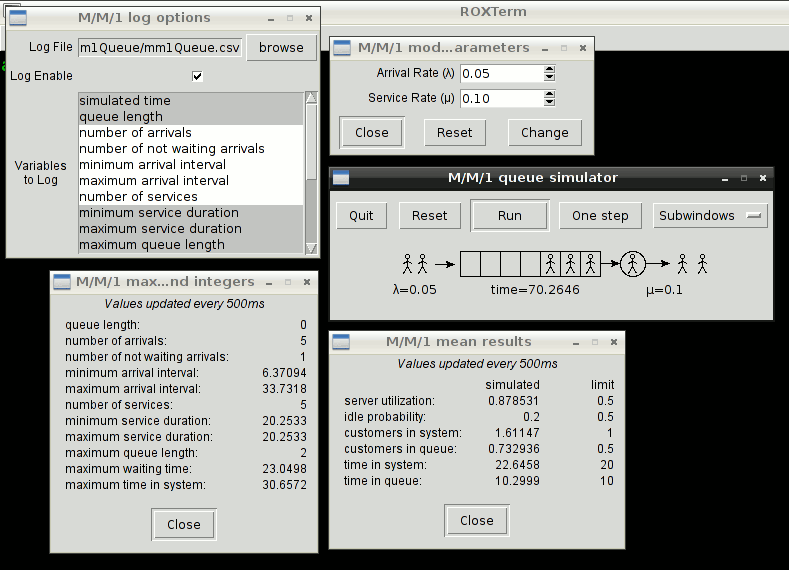
Main features
- Easy to use graphical user interface. Allows to start, stop, pause and stepping through a simulation.
- System parameters (λ, µ) can be dinamically changed during a simulation.
- Computes the results of the M/M/1 analytical model for stable systems.
- Allows simulating an unstable system. This is only useful to demonstrate what happens. In this case the program must be interrupted before the queue becomes too long and the simulation gets slower and slower.
- Logging capabilities. You can choose what variables to log and enable/disable logging at runtime. A comma separated values (CSV) log file format is used. That can be opened and edited by any spreadsheet.
- Portable. Runs unmodified on Win, MacOS and many flavours of Unix (including Linux and FreeBSD) because it is based on Tcl/Tk.
Simulation results
| variable | short description | long description |
|---|---|---|
| Model parameters. | ||
| arrRate | arrival Rate | Arrival rate is the average number of arrivals per time unit. It is the inverted value of the average interval between two adjacent arrivals. |
| servRate | service Rate | Service rate is the average number of completed services per time unit, provided there are always customers in the queue. It is the inverted value of the average service duration. |
| Maximum, minimun and counters values. | ||
| numArr | number of arrivals | Total number of arrivals to the system. The difference NumArr-NumServ represents the customers in the system at the end of simulation. This number is used to compute the simulated idle probability (p0Sim). |
| noWait | number of not waiting arrivals | Total number of customers that have been served immediately after their arrival. |
| minInt | minimum arrival interval | Smallest generated interval between two adjacent arrivals. |
| maxInt | maximum arrival interval | Largest generated interval between two adjacent arrivals. There is no limit on this in the M/M/1 theoretical model, so it can be very large, although higher values are less probable. |
| numServ | number of services | Total number of completed services. The difference NumArr-NumServ represents the customers in the system at the end of simulation. This number is used to compute the average times (wsSim and wqSim). |
| minServ | minimum service duration | Smallest generated service duration. |
| maxServ | maximum service duration | Largest generated service duration. There is no limit on this in the M/M/1 theoretical model, so it can be very large, although higher values are less probable. This value should be much smaller than the experiment duration. |
| maxQlen | maximum queue length | Largest number of customers in the queue, not including the one being served. |
| maxWait | maximum waiting time | Largest time spent in queue (of those whose service has started). |
| maxSystem | maximum time in system | Largest time spent in the system (of those served). |
| Average values and probabilities | ||
| roSim | server utilization | Server utilization = Probability, that the server is busy = (1 - Probability that the server is idle) = Traffic rate. Traffic rate is computed as a ratio arrRate/servRate. |
| p0Sim | idle probability | Probability, that the arriving customer does not wait = Probability, that the system is empty = 1 - Probability that the server is busy. |
| lsSim | customers in system | Average number of customers in the system (including the one being served). |
| lqSim | customers in queue | Average number of customers in the queue (average queue length including empty queue intervals). |
| wsSim | time in system | Average time spent in the system (average of waiting + service time). |
| wqSim | time in queue | Average time spent in the queue (average waiting time including zero - no waiting - values). |
Limit average values and probabilities
Analytical results found for an M/M/1 system are summarized by the following formulas:
roLimit=arrRate/servRate
p0Limit=1-roLimit
lsLimit=roLimit/p0Limit
lqLimit=lsLimit*roLimit
wsLimit=1/(servRate-arrRate)
wqLimit=wsLimit*roLimit
These are limit values that means they only make sense if the system is stable (roLimit<1).
Pseudo-random number generation
Random numbers required by the simulation of an M/M/1 queue system must have an exponential distribution and are generated starting from the rand() function built into Tcl expr(n) command. The following formula is used:
1/λ log(1-rand())Here rand() returns a pseudo-random floating-point value in the range (0,1) and λ is the distribution parameter. The generator algorithm provided by Tcl is a simple linear congruential generator. Each result from rand completely determines all future results from subsequent calls to rand. The seed of the generator is initialized from the internal clock of the machine.
For optimization purposed the previous formula has been implemented as::
λ-1 log(rand())
This saves a subtraction and uses a multiplication instead of a division (which is a bit faster).
Control logic
The following UML statechart describes how the functions of the control buttons are implemented:
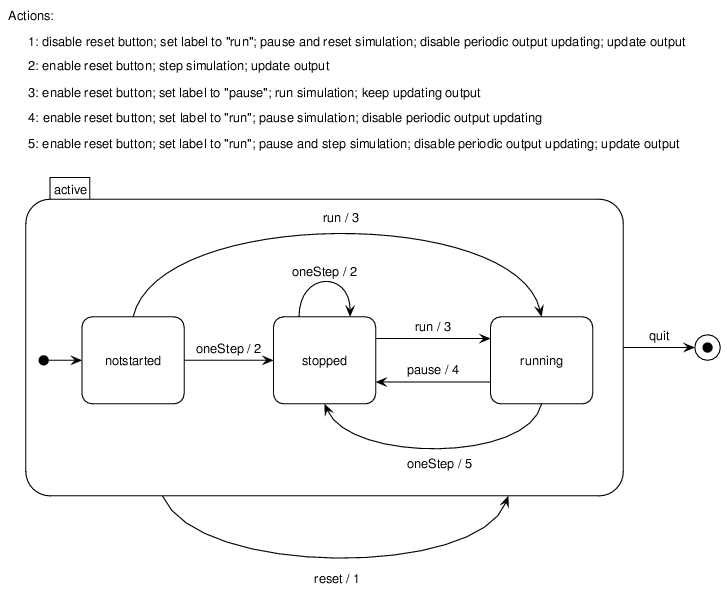
The control logic of the buttons panel. TCM source of this diagram is also available.
The above diagram shows there are only three states of the system: the simulation can only be not yet started or stopped (not running) or not stopped (running). There are four control buttons: quit, reset, run/pause and one step. While run/pause and one step are always enabled, reset is not. The purpose of the reset button is to abort the current simulation and begin a new one without having to restart the entire program.
FAQ
- How do I run it?
-
Because mm1Queue is a GUI app the text-only Tcl shell won't suffice. You need the windowing shell included with the Tk windowing toolkit.
To run the program under Unix (Linux and Mac OS X included), ensure that the executable bit is setted:
$ chmod +x main.tcl
then do:$ ./main.tcl
If this doesn't work make sure the tk package is installed. You can also try
$ wish main.tcl
or you can change the path for wish(1) by editing this line of main.tcl:exec wish "$0" "$@"
- I 'd like to know if the unit time of the timer on the window that correspond to queue schema (time=xxx, under the shema of queue) is in "secondes" or "ms"?
-
There are not unit measures, I know. This may seem wrong but was done purposely. You can take time values as seconds, or milliseconds or half-seconds or whatever you want. All other quantities will be referred to this time unit you have chosen.
E.g. if you assume time is in seconds, arrRate will be measured in 1/s; if you take it as ms, you'll have to input arrRate in 1/ms or ms^-1 or 10^-3s.
- Can I contribute to mm1Queue development? What skills do I need?
-
You're welcome. I run a pretty busy life and I've almost abandoned it. You may want to take the time to study the Tcl language. It's fun & easy even if you have not programmed before :-)
The official Tcl tutorial and this by the Bin-Co smart folks will help you grasp all the required Tcl/Tk knowledge you need while also having some fun. If you also know a bit of queue theory you are then ready to take over maintenance and development of mm1Queue.
TODO list
There are many ways the simulator can be improved starting from this first version. This is my current TODO list:
- Provide a command line interface so that the simulator can be controlled within scripts with no user interaction.
- Add a synchronized simulation mode that animates the queue representation. Useful mainly for demonstrative purposes
- In addition to FIFO other service types should be implemented (LIFO, SIRO and priority queues).
- Add functions to save the state of the simulation to a file and load a saved simulation.
- Allow the user to choose a probability distributions between M,D or Ek or define an arbitrary distribution through a formula or graphically.
- Implement generic G/G/s/A/B queue system simulation.
- Extend the simulator to handle queue networks.