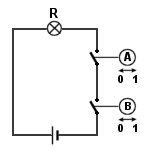
Figura 3.1. Il circuito logico AND in versione elettro-meccanica.
1 Complemento a 2
2 Divide-et-impera
3 Il sommatore di 2 bit
4 Black-box
5 Il sommatore di 3 bit
6 Il sommatore di n bit
7 Il sommatore algebrico
8 Overflow e Underflow
La ragione per cui i calcolatori utilizzano il sistema posizionale binario, invece del sistema posizionale decimale a noi più familiare, è solamente tecnologica. È molto più semplice costruire dispositivi per il calcolo e la memorizzazione con due stati anziché con dieci stati differenti.
Quella che segue è la rappresentazione di numeri binari con segno in complemento a due, per semplicità effettuata su sole 3 cifre binarie.
011 3 010 2 001 1 000 0 111 -1 110 -2 101 -3 100 -4
Su 3 bit si possono rappresentare 23=8 numeri differenti. Esiste una sola rappresentazione dello zero e questo è un importante fattore di semplicità. Un altra proprietà notevole del complemento a 2 è che l'ultimo bit assume il significato di bit del segno: vale 0 se il numero è positivo ed 1 se è negativo.
Questa strana rappresentazione circolare viene usata perchè semplifica la circuiteria che si occupa di effettuare le operazioni aritmetiche (ALU). Infatti una sottrazione viene trasformata in una addizione.
Ad esempio:
2 - 2 + 010 + 3 = <=> -3 = <=> 101 = ---- ---- ------ -1 -1 111
A volte accade che si ottiene un bit in più di riporto (carry) il quale va ignorato:
3 - 3 + 011 + 1 = <=> -1 = <=> 111 = ---- ---- ------ 2 21010
In sostanza in complemento a 2 le somme algebriche si effettuano con le consuete regole di somma e riporto di bit dell'addizione binaria, avendo cura di utilizzare lo stesso numero di bit per ciascun operando e ignorando il bit in più posto all'estrema sinistra che potrebbe scaturire uguale ad 1 dall'operazione.
Questo è vantaggioso dal punto di vista hardware, perché non occorre una circuiteria separata per effettuare la sottrazione: si può riutilizzare facilmente la stessa circuiteria dell'addizione, semplicemente occorre complementare (a 2) il sottraendo e poi si effettua la somma tra minuendo e sottraendo, cancellando il primo 1 a sinistra. L'operazione di complemento a 2 è molto facile per un calcolatore, come vedremo al ¶ 7.
In fase di input/output (I/O) il calcolatore dovrà convertire dalla rappresentazione di un numero come sequenza di caratteri, secondo un certo codice, ad es. ASCII, a quella in complemento a 2 e viceversa.
Ad es. nel caso dell'output l'algoritmo per stampare un numero con segno contenuto nella variabile A sarà il seguente, espresso in lingua italiana:
Questo algoritmo fa uso del fatto che dividendo ripetutamente per 10 si ottengono le cifre nella base 10 in ordine inverso. L'algoritmo termina quando il risultato della divisione è zero.
Per convertire un numero in base 10 in base 2 si divide ripetutamente per 2, svolgendo i calcoli in base 10, finché non si ottiene zero. Giustapponendo i resti nell'ordine in cui si ottengono da destra verso sinistra, si ottiene il numero equivalente in base 2. Questo si chiama metodo delle divisioni ripetute per la base (di destinazione). Il calcolatore usa lo stesso metodo, ma per convertire da base 2 a base 10, quindi la base di destinazione per cui dividere ripetutamente è 10, e svolge internamente i calcoli in base 2.
Ho consultato vari libri introduttivi sull'argomento, ma non ne ho trovato nessuno che riporti un ragionamento che dimostri le proprietà operatoriali della rappresentazione in complemento a 2, perciò ho deciso di sviluppare questo ragionamento io stesso, perché lo ritengo particolarmente importante e significativo per la comprensione del motivo per cui le somme in complemento a due funzionano, ossia danno il risultato corretto, e perché bisogna ignorare il riporto. Se siete tra quelli che vogliono sapere il perchè delle cose, continuate a leggere, altrimenti se siete pigri, o se conoscete già il motivo, saltate al ¶ 2.
Siano A e B due numeri di n=3 bit. La scelta di porre n=3 non è limitativa: il ragionamento si può facilmente generalizzare per n qualsiasi. A e B saranno formati dalla giustapposizione di 3 bit, eventualmente alcuni potranno essere nulli, ma in generale dobbiamo rappresentarli lo stesso, percui poniamo A=A2A1A0 e B=B2B1B0.
Vogliamo effettuare l'operazione di sottrazione A-B, ma non vorremmo utilizzare il complicato metodo dei prestiti, algoritmo che sicuramente vi è noto in base 10 dalle scuole elementari e che funziona in modo analogo in base 2 (o qualsiasi altra base in un sistema posizionale).
Premettiamo un paio di semplici definizioni: si dice complemento a 1 di un numero binario B su n bit la quantità c1(B,n)=(2n-1)-B. Le parentesi sono pleonastiche. Una volta fissato n, la quantità entro parentesi è una costante, così per n=3 avrò c1(B)=7-B. Per semplicità ometto la dipendenza da n, assumendo che n abbia sempre lo stesso valore nella nostra discussione (scrivo una volta per tutte a parte il valore di n).
Si noti che 2n-1 è il numero binario che precede 2n. 2n si rappresenta come 1 seguito da esattamente n zeri in binario, quindi 2n-1 è un numero che si rappresenta in binario come n volte uno.
Per esempio per n=3 ho c1(B)=111(2)-B. È chiaro quindi che c1 si può ottenere anche invertendo tutti i bit di B, definendo 0 come l'inverso di 1 e viceversa.
Quest'ultimo fatto vale solo perché ci sono solo due cifre, ossia siamo in base 2. In basi superiori non ha senso parlare di inversione di cifre. Ad esempio in base 10, il complemento a 1 di un numero B su n cifre decimali è c1(B)=(10n-1)-B. Così se ad es. n=2, ho 102-1=99 e se pongo B=40, il risultato è c1(40)=99-40=59.
In tal caso di ottiene il c1 sottraendo da 9 ogni cifra, ma 5 non è l'inversa di 4, e nemmeno 0 è l'inversa di 9. In generale in una base b si ottiene il c1 di un numero sostituendo ogni sua cifra con b-1 meno la cifra considerata.
Altra definizione: il complemento a 2 di un numero B in base 2 su n bit: c2(B)=2n-B=1+c1(B).
Il fatto che ci sia l'operatore meno davanti alla B nella definizione di complemento a 1 e quindi anche in quella di complemento a 2, e il fatto che vogliamo fare la differenza A-B, ci suggerisce di provare a vedere che succede se, presi due numeri binari positivi A e B rappresentati in forma naturale su n=3 bit, facciamo A+c2(B). Questa operazione equivale e A+(23-B), o, per la proprietà associativa, (A+23)-B e in generale si può indicare in questo modo:
1 A2 A1 A0 - B2 B1 B0 = ------------- R2 S2 S1 S0
Si noti che questa sottrazione dà sempre un numero R2S2S1S0 positivo.
Ora supponiamo che A>=B. Allora si avrà S=S2S1S0=A-B>=0 e R2=1. Se ignoro R2 ho che S è il risultato corretto e, cosa importantissima, posso fare la sottrazione A-B come se fosse un'addizione, facendo A+c2(B), usando il semplice algoritmo della somma!
Ma aspettate un momento! Resta ancora da vedere se le cose vanno bene per A<B. Oggi è il nostro giorno fortunato perché A+23-B=23+(A-B)=23-(B-A) e questo è esattamente il complemento a 2 (sempre su 3 bit) di B-A>0 per l'ipotesi equivalente che A<B.
Questo significa che, sempre nell'ipotesi A<B, S=S2S1S0 è il complemento a due di B-A>0 su 3 bit. Si noti inoltre che in tal caso R2=0, proprio perché l'uno più significativo del minuendo viene prestato per poter effettuare la sottrazione.
Questo ci suggerisce che se rappresentiamo i numeri binari negativi come il complemento a 2 dei rispettivi positivi sullo stesso numero n di bit, possiamo eseguire le sottrazioni semplicemente con lo stesso algoritmo della somma di numeri positivi, ignorando il riporto Rn ed effettuando la complementazione a 2 del sottraendo. Difatti, con questa rappresentazione dei negativi, A-B equivale a A+c2(B). In particolare abbiamo visto che se A-B deve essere minore di zero perché A<B, allora A+c2(B) su n bit viene fuori un numero negativo correttamente rappresentato in c2.
In effetti anche nel sistema decimale si può utilizzare la rappresentazione in c2 dei numeri negativi e le differenze diventano così delle somme. Ad es. si consideri 3-4 su n=2 cifre decimali. Ho: c2(4)=102-4=100-4=96 e quindi la sottrazione diventa la seguente somma: 3+96=99. Inverto il segno di 99 per vedere a quale negativo corrisponde: c2(99)=102-99=1, quindi 99 rappresenta -1!
Da notare che la scelta di quanti positivi o quanti negativi avere è arbitraria. Tuttavia si preferisce avere un negativo in più per conservare la proprietà che l'ultimo bit indichi il segno del numero.
Facciamo il progetto logico di un sommatore di numeri binari in formato naturale di 3 cifre (o bit), che, per quello detto al ¶ 1, effettua correttamente anche le somme algebriche di numeri di 3 bit in formato complemento a 2.
Quante sono tutte le possibili combinazioni dei due operatori? Poiché su 3 bit ogni operatore può essere scelto tra 23=8 possibili, ho 8 modi di scegliere il primo operando e per ogni scelta del primo ho altre 8 possibili scelte del secondo, per un totale di 8x8=64 possibili combinazioni di due operatori di 3 bit.
Per semplificare la progettazione suddivideremo il nostro sistema in sottosistemi collegati opportunamente tra loro e in grado di sommare solo due o tre cifre binarie per volta. Il progetto di questi sottosistemi risulta più semplice, in quando su 2 e 3 bit i casi di somma possibili sono rispettivamente solo 2x2=4 e 2x2x2=23=8.
Il primo sottosistema viene detto addizionatore (o sommatore) semplice o anche semiaddizionatore, semisommatore, mezzo sommatore o sommatore a 1 bit (half adder in inglese) ed è un dispositivo che, comunque realizzato deve obbedire alla tabella di regole aritmetiche 3.1.
| A | B | R | S |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Tabella 3.1. Tabella aritmetica delle regole di somma di 2 bit.
A e B sono numeri binari di una sola cifra, mentre S rappresenta la loro somma e R un eventuale riporto.
La funzione logica (od operatore) che mette in corrispondenza la coppia (A, B) con il riporto R viene spesso detta AND logico, per il fatto che rappresenta la congiunzione logica o connettivo logico e, che nel linguaggio comune collega due proposizioni per ottenerne una composta, che sarà vera se e solo se entrambe le proposizioni collegate sono vere.
Le colonne A,B,R della Tabella 3.1 forniscono quindi la tavola o tabella di verità del connettivo AND, la quale mostra per via estensiva, cioè analizzando tutti i casi possibili, il valore di verità di A AND B in funzione dei valori di verità di A e B.
Il collegamento o l'analogia tra logica ed aritmetica binaria si ottiene facendo corrispondere ai valori di verità vero e falso (in inglese true e false rispettivamente) di una proposizione, rispettivamente le cifre binarie 1 e 0, ossia alla tabella aritmetica 3.1 la corrispondente tabella di verità 3.2.
| A | B | R (A and B) |
S (A xor B) |
|---|---|---|---|
| f | f | f | f |
| f | t | f | t |
| t | f | f | t |
| t | t | t | f |
Tabella 3.2. Tabella di verità dei connettivi AND (R) e XOR (S).
In questa tabella per semplicità il valore vero è stato rappresentato con una t e il valore falso con una f.
Utilizzando una tecnologia che faccia uso della pila, inventata dal fisico italiano Alessandro Volta nel 1799 per convertire l'energia interna chimica in energia elettrica (o di altre pile più moderne ed efficienti, ancora di tipo voltaico oppure diverso) e della lampadina ad incandescenza, ideata nel 1879 dall'inventore statunitense Thomas Alva Edison (o di altre lampadine più moderne, come i diodi emettori di luce, i cosiddetti LED), che trasforma l'energia elettrica in energia luminosa percepita dai nostri occhi, e aggiungendo un dispositivo meccanico in grado di interrompere e ripristinare il passaggio di corrente in un circuito elettrico quando viene azionato (un interruttore), possiamo costruire facilmente una macchina elettro-meccanica che sia in grado di calcolare il riporto della somma di due bit (Fig. 3.1).
Si tratta di un circuito elettrico costituito da una pila alla Volta, oppure un altro tipo di generatore, una lampadina R in funzione di utilizzatore di energia e due interruttori A e B azionabili indipendentemente.
Questo circuito elettrico rappresenta un vero e proprio modello fisico dell'operazione logica AND e perciò viene anche detto circuito logico. Infatti se, per esempio, si conviene di associare ai due stati di un interruttore, che sono aperto e chiuso, rispettivamente i valori di verità falso e vero o le cifre binarie 0 e 1 e si conviene di associare ai due stati della lampadina spenta e accesa rispettivamente falso o 0 e vero o 1, gli stati dei due interruttori A e B determinano quello della lampadina R esattamente secondo le tabelle di verità 3.1 e 3.2 viste prima. Infatti affinché il circuito sia chiuso e quindi si accenda la lampadina devono essere chiusi entrambi gli interruttori.
Come si usa questo semplicissimo calcolatore? L'operatore umano imposta i due interruttori A e B sui valori di bit desiderati, fornendo così l'input alla macchina, e poi, dopo qualche istante necessario affinché si stabilizzi la corrente nel circuito, legge il riporto della somma, che rappresenta l'output, semplicemente guardando se la lampadina è accesa o spenta.
La colonna S della somma di bit (Tabella 3.1) realizza invece l'operazione logica di disgiunzione esclusiva (la famosa locuzione aut ... aut ... dei latini ribattezzata in tempi recenti XOR) che è vera solo se le proposizioni A e B sono vere, ma non se lo sono entrambe.
Il circuito elettromeccanico equivalente sarà leggermente più complicato, sia dal punto di vista meccanico che elettrico.
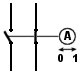 Una prima soluzione consiste nell'utilizzare degli
interruttori invertitori, che si trovano realmente in
commercio. Si tratta di un interruttore doppio, ma i due
interruttori singoli che comprende non sono indipendenti tra loro:
quando uno è aperto, è sicuro che l'altro è
chiuso e viceversa, perchè l'uno trascina l'altro. Proprio
perché gli stati dei due interruttori sono uno l'opposto
dell'altro, non possono mai avere lo stesso stato, questo
dispositivo quadripolare (cioè a 4 morsetti) è detto
invertitore.
Una prima soluzione consiste nell'utilizzare degli
interruttori invertitori, che si trovano realmente in
commercio. Si tratta di un interruttore doppio, ma i due
interruttori singoli che comprende non sono indipendenti tra loro:
quando uno è aperto, è sicuro che l'altro è
chiuso e viceversa, perchè l'uno trascina l'altro. Proprio
perché gli stati dei due interruttori sono uno l'opposto
dell'altro, non possono mai avere lo stesso stato, questo
dispositivo quadripolare (cioè a 4 morsetti) è detto
invertitore.
Per realizzare il circuito logico XOR è facile convincersi che occorrono due invertitori collegati in parallelo "incrociato" come in Figura 3.2.
In alternativa si può ricorrere a un paio di interruttori tripolari detti in gergo deviatori, ancora collegati in modo incrociato (Figura 3.3).
Stavolta il numero di morsetti da collegare risulta ridotto (6 invece di 8).
Infine per realizzare un half-adder si possono per esempio combinare in uno solo i due circuiti delle figure 3.1 e 3.2, in una specie di parallelo meccanico ed elettrico, ottenendo una meccanica di interruzione mostrata in Figura 3.4.
Oppure possiamo utilizzare dei deviatori doppi e a due posizioni, per semplificare ulteriormente il circuito come in Figura 3.5.
Dovrebbe essere chiaro dal ¶ 3 che siamo in grado di realizzare circuiti logici con tecnologia elettromeccanica comunque complicati, senza alcuna difficolta, almeno in teoria.
In realtà la tecnologia elettromeccanica non è adatta alla realizzazione di calcolatori non banali. La tecnologia elettronica i cui sviluppi risalgono solamente al secolo scorso, permette invece di realizzare calcolatori complicati, veloci, affidabili, in spazi molto ridotti.
Non tratterò i principi fisici su cui si basa la tecnologia elettronica in questo articolo, anche se sono interessanti, perché questo ci farebbe fare una lunga digressione. Piuttosto quello che mi preme sottolineare in questo contesto è che la logica che queste macchine implementano è del tutto indipendentemente dalla tecnologia usata. In futuro è possibile che altre tecnologie soppiantino la tecnologia elettronica, realizzando con maggiore efficienza e convenienza le stesse funzioni logiche!
Così un half-adder resta sempre un half-adder, qualunque sia la tecnologia con cui viene realizzato. Anche se doveste cambiare la base di numerazione, potete avere half-adder per un'altra base, ad es. la base dieci.
Restando sulla base 2, per le ragioni tecnologiche esposte all'inizio di questa lezione, un half-adder, comunque sia realizzato, può essere visto come un sistema con due segnali binari in ingresso (gli stati degli interruttori A e B in Figura 3.4) e due segnali binari in uscita (gli stati delle lampadine R e S nella stessa Figura 3.4). Nella Figura 4.1 abbiamo rappresentano l'half-adder come un blocco etichettato col simbolo di sommatoria.
Questa schematizzazione è detta della scatola nera (black-box) perché è come se la nostra macchina fosse racchiusa dentro una scatola complementamente opaca, dentro la quale non possiamo (o non vogliamo) guardare, mentre tutto quello che ci interessa o che possiamo sapere è il suo comportamento esterno, il modello matematico che ci dice come come l'uscita o le uscite sono legate all'ingresso o agli ingressi, che ci permette di prevedere in modo univoco il valore delle uscite una volta noto il valore degli ingressi. Questo modello matematico nel caso dell'half-adder è fornito appunto dalla Tabella 3.1 oppure dalle corrispondenti equazioni dell'algebra di George Boole:
R=A and B S=A xor B
Perciò d'ora in poi non ci sforzeremo più di disegnare circuiti elettromeccanici;. Il nostro progetto è del tutto indipendente dalla tecnologia usata e difatti il sommatore che progetteremo potrà essere realizzato anche con la moderna tecnologia elettronica allo stato solido. Noi progetteremo il sistema, sicuri che esso sarà poi realizzabile con qualche tecnologia.
Così possiamo studiare i sistemi limitatamente al loro comportamento esterno (o relazione input/output). Possiamo connettere in qualche modo sistemi di cui conosciamo il comportamento esterno e chiederci come si comporterà il sistema più complesso così ottenuto, una volta che ne siano definiti ingressi ed uscite, senza preoccuparci troppo di come le connessioni saranno poi realizzate a livello tecnologico.
Ad esempio se adottiamo il punto di vista della black-box possiamo subito riconoscere che un half-adder può essere costruito a partire da due blocchi che realizzano le funzioni logiche di AND e XOR e che condividono gli ingressi, secondo lo schema a blocchi di Figura 4.2
Se si considera il sistema complessivo, in realtà questa volta stiamo guardando dentro la scatola, ma quello che vediamo non è esattamente come è fatto il dispositivo, ma un altro schema a blocchi, in cui ogni blocco corrisponde ad una porzione del dispositivo finale. Difatti non è difficile riconoscere come i due rami in parallelo di Figura 3.4 oppure 3.5 corrispondano ai blocchi etichettati con & e ^ di Figura 4.2, che realizzano rispettivamente le funzioni di AND e OR logico.
L'idea è di sfruttare un certo numero di half-adder, vedremo che ne occorrono almeno 2, collegati opportunamente, per costruire un sommatore di 3 bit o full-adder.
Le prime due cifre possono essere sommate con un half-adder, generando una somma che chiamiamo S' e un riporto R', come in Figura 5.1.
Poi inseriamo in cascata un altro half-adder per sommare R e S', ottenendo un riporto R'' e una somma S'' (Figura 5.2).
Sommando 3 bit il risultato può essere al massimo di 2 bit. Infatti la somma che dà il numero più grande è la somma di 3 uno:
A + 1 + B + 1 + R = 1 = ---- ---- RoS 11
Abbiamo indicato il riporto in uscita con Ro (R pedice o, o sta per output) e non con R, per evitare che qualcuno possa fare confusione con l'ingresso R, in quanto in generale non sono uguali. Avremmo anche potuto usare una lettera differente, ma R era troppo comoda perché ricorda che si tratta di un riporto.
Dobbiamo quindi avere solo 2 uscite. Attualmente in Figura 5.2 ne abbiamo 3! Esse sono R', R'' e S''. È chiaro quindi che il nostro sistema non è ancora completo.
Osserviamo che se R'=1 vuol dire che per forza A=B=1 e quindi questo implica che S'=0, da cui ancora si deduce che R''=0.
Se invece supponiamo che R'=0, allora R'' può essere sia 0 che 1.
Quindi R' e R'' non possono mai valere contemporaneamente 1: o valgono entrambi zero, oppure uno vale 1 e l'altro 0. Per questa ragione, possiamo evitare di impiegare un altro half-adder e semplificare il circuito. La somma di R' e R'' in tutti e tre i casi possibili è data dalla Tabella 5.1.
| R' | R'' | R'+R'' |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
Tabella 5.1. Tabella aritmetica della somma dei resti degli half-adder di un full-adder.
Osserviamo che la Tabella 5.1 coincide con le prime tre righe della Tabella 5.2 di un OR logico.
Perciò completiamo il full-adder inserendo un blocco logico OR con ingressi R' e R''. Questo nuovo sottosistema non avrà mai in ingresso valori entrambi uguali ad 1, quindi nessun valore significativo viene perso nella somma. Le uscite che restano, battezzate S e Ro, saranno rispettivamente la somma e il riporto della somma di 3 bit.
D'ora in poi indicheremo un full-adder con un box etichettato con un simbolo di sommatoria, eventualmente con un pedice numerico, come in Figura 5.4.
Credo che questo paragrafo abbia esemplificato sufficientemente l'utilità del punto di vista della black-box esposto al ¶ 4. Lavoreremo a livello di box anche nel prossimo paragrafo.
Poniamo per semplicità n=3, ma questo non è limitativo. Considerate l'algoritmo che eseguite manualmente quando sommate dei numeri binari di 3 bit, che è del tutto analogo a quello che usate in base 10.
Si tratta di incolonnare i numeri. Poi iniziate a sommare le cifre più a destra A0 e B0, ovvero quelle meno significative, ottenendo la cifra più a destra S0 del risultato e un riporto R0. Questo è il lavoro di un half-adder, progettato nel ¶ 3. (Figura 6.1)
Poi avete da sommare le due cifre di peso 21 A1 e B1 con in più un eventuale riporto R0 della somma precedente, che eventualmente può essere zero. Si tratta di sommare 3 cifre binarie e questo lo possiamo fare col full-adder del ¶ 5. (Figura 6.2)
Infine sommiamo le due cifre di peso 22 e il riporto dalla somma precedente tramite un altro full-adder. (Figura 6.3)
È chiaro come si continua per sommare numeri di 4, 5, 6, ..., n bit. Indicheremo un sommatore di numeri a 3 bit con lo schema a blocchi di Figura 6.4.
Nel ¶ 6 abbiamo visto da quali parti potrebbe essere fatta una macchina in grado di eseguire la somma di due numeri qualsiasi di n bit. Abbiamo usato principi di progettazione modulare. È notevole il fatto che la progettazione modulare si applichi tanto bene sia all'hardware che al software!
Adesso cercheremo di ricavare lo schema a blocchi di una macchina in grado di eseguire somme algebriche, quindi sia addizioni che sottrazioni di numeri ad n bit (sommatore/sottrattore o sommatore algebrico). Anche questa volta poniamo n=3 e questo non è limitativo perché è facile estendere i risultati per n generico.
Come detto al ¶ 1, per eseguire la sottrazione in complemento a 2 occorre complementare a 2 il sottraendo (nel nostro caso B=B2B1B0) e poi eseguire la somma normalmente.
Complementare ad 1 un numero è piuttosto semplice, occorre un blocco invertitore per ciascun bit, come in Figura 7.1.
L'invertitore, detto anche negatore, NOT, è un blocco che realizza la negazione logica o connettivo non. In Figura 7.2 sono riportati due circuiti logici elettromeccanici che realizzano questa funzione. Così siamo sicuri che è possibile realizzare un negatore.
A noi serve però il complemento a 2, che si ottiene aggiungendo 1 al complemento a 1. Piuttosto che progettare due blocchi distinti, un complementatore a 2 di 3 bit e un sommatore di 3 bit e poi collegarli insieme, stavolta conviene procedere in maniera diversa: si può pensare di sostituire l'half-adder nel sommatore a 3 bit di Figura 6.3 con un full-adder e per mezzo del suo ingresso R, il nuovo ingresso che si rende disponibile, fornire l'1 che serve per la complementazione a 2 come un primo riporto iniziale.
In formule sappiamo che A-B=A+c2(B). Invece di calcolare subito c2(B), stiamo spezzando l'operazione c2 di complemento a 2 in questo modo: A-B=A+c1(B)+1.
Oltre ai due numeri, aggiungiamo quindi una linea di input binaria chiamata op che serve per selezionare il tipo di operazione da eseguire, secondo la semplice Tabella 7.1.
| op | operazione |
|---|---|
| 0 | addizione |
| 1 | sottrazione |
Tabella 7.1. Convenzione per la selezione dell'operazione del sommatore algebrico.
La scelta di rappresentare con zero l'operatore di addizione e con uno quello di sottrazione anziché viceversa non è casuale, ma è quella che più semplifica il circuito finale di Figura 7.3 perché in questo modo si può portare il segnale op direttamente su R in quanto i valori coincidono, senza necessità di inversioni.
La Tabella 7.2 indica come ogni singolo bit del sottraendo B, indicato con la notazione Bi, debba essere mutato in Bi a seconda del valore di op.
| op | Bi | Bi |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Tabella 7.2. Complementazione a richiesta di un bit del sottraendo.
Si noti che questa è la tabella di uno XOR aritmetico. Occorre quindi una fila di blocchi XOR per effettuare la complementazione a richiesta tramite il valore di op. In effetti è una proprietà generale dell'OR esclusivo quello di trasmettere inalterato un bit in ingresso se l'altro viene posto a zero, e di invertirlo se invece l'altro bit viene posto ad uno. Tutte queste osservazioni ci permettono di ricavare il circuito finale di Figura 7.3.
È in questo modo che funzionano le istruzioni assembler per sommare e sottrarre due numeri (ADD e SUB in assembly Intel 386+). Questo è l'algoritmo per effettuare le somme algebriche con la rappresentazione in complemento a 2, algoritmo che è cablato nell'hardware della macchina.
L'ingresso op è un esempio di ingresso di controllo o di selezione dell'istruzione, che indica il tipo di operazione da eseguire, piuttosto che i dati su cui eseguire l'operazione.
Il sommatore algebrico che abbiamo progettato è un esempio molto semplice di unità aritmetico-logica (ALU, Arithmetic Logic Unit). Le ALU realmente in commercio sono in grado di eseguire molti più tipi di operazioni oltre alla somma e alla sottrazione. Come dice il nome, una ALU, è in grado di eseguire anche operazioni logiche, oltre che aritmetiche. Per selezionare più di due operazioni occorre più di un bit di controllo, quindi in una ALU più complessa vi saranno più bit di controllo. Saranno comunque sempre presenti due sole file di bit in ingresso e una di bit in uscita come nel nostro semplice sommatore.
Riprendiamo la rappresentazione in c2 su 3 bit vista al ¶ 1. Poiché con 3 bit possiamo rappresentare solo 8 numeri differenti (nella fattispecie lo zero, 3 numeri positivi e 4 negativi), l'insieme numerico ottenuto è composto da un numero finito di elementi. Non possiamo rappresentare l'insieme infinito dei numeri interi come quello con cui si lavora in matematica, perché ci occorrerebbe un numero infinito di bit e fisicamente non possiamo realizzare sistemi di memorizzazione o di elaborazione di estensione infinita.
Questo ha delle importanti ripercussioni sulle operazioni aritmetiche, che non sono sempre fattibili come in matematica, dove lavorano invece su insiemi illimitati.
I calcolatori moderni hanno registri per numeri interi di 32 o 64 bit: questo significa che sono in grado di effettuare in modo hardware operazioni tra numeri interi di 32 o 64 bit, che possono essere pochi o più che sufficienti a seconda delle applicazioni. Tuttavia questa non è una limitazione tanto grave perché in modo software si può lavorare con precisione estesa a piacere, nei limiti consentiti dall'estensione della memoria e a scapito naturalmente di una minore velocità di calcolo rispetto a quella dei tipi interi nativi.
Usando numeri interi gestiti direttamente dalle singole istruzioni aritmetiche di codice della CPU ed effettuando tramite queste istruzioni operazioni tra questi, finché il risultato può essere contenuto nei registri di uscita della ALU, risulterà corretto e non sembreranno che ci siano limitazioni sul range dei valori rappresentabili. Ma ci sono valori degli operandi per cui questo non è vero.
Ad es. su 3 bit, considerando la rappresentazione in c2, ossia operando con numeri con segno, non è possibile rappresentare la somma 2+2. Il sommatore algebrico visto al ¶ 7 la calcolerà come segue, ma il risultato, interpretato come un numero in c2, ad es. da una routine per la stampa dell'output, è vistosamente sbagliato:
010 + 2 + 010 = <=> 2 = ----- ---- 100 -4 ^ bit del segno
Infatti abbiamo sommato due numeri positivi (bit del segno 0) e ne abbiamo ottenuto uno negativo (bit del segno 1). Ecco ancora un altro esempio in cui si ha lo stesso problema:
101 + (-3) + 110 = <=> (-2) = ----- ------1011 3 ^ bit del segno
Si noti che la rappresentazione in c2 è circolare. Potete effettuare somme e sottrazioni in c2 partendo dal primo addendo o dal minuendo e percorrendo rispettivamente in senso orario o antiorario un numero di unità date dal secondo addendo o dal sottraendo (Figura 8.1).
Proprio questa circolarità produce gli errori detti di overflow, quando si passa attraverso il settore critico evidenziato in grigio. L'overflow è un problema inevitabile, dovuto al fatto che la rappresentazione si svolge su un numero finito di bit.
È facile convincersi che sommando due numeri di segno opposto non si passa mai attraverso il settore critico, quindi l'errore di overflow si può verificare solo sommando due numeri di egual segno a n bit.
In particolare nel caso di errore quando si sommano due numeri positivi, e si ottiene un risultato negativo, si parla più propriamente di overflow, mentre sommando due numeri negativi, se il risultato è positivo, si parla di errore di underflow. Tuttavia spesso si dice che si è verificato overflow in entrambi i casi e il termine underflow non è molto usato.
La tabella 8.1 rappresenta una funzione logica ov(A2, B2, S2) che ci permette di rilevare la condizione di overflow.
| A2 | B2 | S2 | ov | tipo di traboccamento |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | - |
| 0 | 0 | 1 | 1 | overflow |
| 0 | 1 | 0 | 0 | - |
| 0 | 1 | 1 | 0 | - |
| 1 | 0 | 0 | 0 | - |
| 1 | 0 | 1 | 0 | - |
| 1 | 1 | 0 | 1 | underflow |
| 1 | 1 | 1 | 0 | - |
Tabella 8.1. Tavola di verità del rilevatore di overflow per numeri signed.
In forma algebrica la funzione ov si scrive in questo modo:
ov(A2, B2, S2) = NOT A2 AND NOT B2 AND S2 OR A2 AND B2 AND NOT S2
Essendo la priorità degli operatori in ordine decrescente la seguente: NOT, AND, OR. Purtroppo non si può ulteriormente semplificare, ma non è difficile progettare un blocco per il rilevamento dell'overflow, come parte separata o integrato nel sommatore algebrico di Figura 7.3, basandosi su questa funzione di trasferimento.
Nel caso i numeri vengano considerati come senza segno (unsigned), su 3 bit la rappresentazione è la seguente, coincidente con quella naturale:
111 7 110 6 101 5 100 4 011 3 010 2 001 1 000 0
È chiaro che, siccome anche le sottrazioni vengono fatte come somme, previa complementazione a 2 del sottraendo, il fatto che una determinata operazione abbia determinato overflow o meno dipende anche da quale delle due operazioni (somma o differenza) è stata effettuata. Per esempio:
001 + 1 + 1 - 111 = <=> 7 = <=> 1 = ------ --- ---1000 0 0
In questo esempio se stavamo facendo una somma, allora abbiamo avuto overflow, ma se stavamo facendo una sottrazione, il risultato è corretto.
Conviene allora che studiamo separatamente il caso di overflow per la somma e la sottrazione, per poi eventualmente unire le condizioni in una sola.
Si noti che il risultato di una somma è sempre corretto se si considera anche il bit R2 davanti a S2S1S0. Nell'esempio precedente 1000(2)=8 era il risultato corretto.
Questa è la ragione per cui abbiamo fatto uscire anche il bit R2 dalla scatola del sommatore in Figura 7.3. Mentre nel caso di numeri signed R2 è del tutto inutile se si considera il risultato, non ne è parte e si può ignorare, nel caso di numeri unsigned, è proprio questo bit che indica la condizione di overflow per la somma.
Con numeri unsigned l'underflow non si può mai verificare, perché gli operandi sono sempre positivi e il risultato va interpretato come un numero positivo.
Qual'è invece la condizione di overflow per la sottrazione di numeri unsigned? Naturalmente quando il minuendo è minore del sottraendo, perché in tal caso il risultato è negativo. Per quello detto alla fine del ¶ 1, A-B=A+c2(B) e se A<B in tal caso R2=0. Quindi R2=0 è la condizione di overflow per la differenza di numeri unsigned.
Possiamo riunire i risultati ottenuti come in Tabella 8.2.
| op | R2 | cy |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Tabella 8.2. Tavola di verità del rilevatore di overflow per numeri unsigned.
In Tabella 8.2, op segue la convenzione di Tabella 7.1. cy sta per carry (riporto) ed è questo il nome che viene di solito dato al bit di overflow per numeri unsigned. Quando cy vale 1 vuol dire che c'è stato un riporto che trabocca oltre la somma di unsigned oppure un prestito mancante per la sottrazione di unsigned. Analiticamente:
cy(op, R2)=op XOR R2
I bit di ov e cy sono effettivamente presenti nel registro flag delle CPU Intel i386+ e vengono settati come da noi descritto dalle istruzioni ADD e SUB dell'assembly i386+. Alcune altre istruzioni utilizzano il valore di questi flag, ad es. le istruzioni di salto condizionato JO (Jump if Overflow) e JC (Jump if Carry), fanno saltare l'esecuzione del codice alla locazione di memoria specificata solo se rispettivamente è uguale ad uno il bit ov e cy.